The MEDITS packages was realized to work with survey data in the format of the MEDITS project. The package uses TA-, TB-, and TC-like tables. Functions using TE and TL table are not already implemented. TA table contains hauls’ information; TB contains catch data; TC contains aggregated biological data. Examples of TA, TB and TC table were added to the package in order to execute the example codes.
You can install the released version of MEDITS from CRAN with:
The MEDITS format uses a specific format for the geographic coordinates. Two functions were introduced to convert the coordinates respectively from the MEDITs format to decimal degrees format and viceversa.
# Coordinates conversion from MEDITS format to decimal degrees
library(MEDITS)
dd <- MEDITS.to.dd(TA)
head(dd)
#> TYPE_OF_FILE COUNTRY AREA VESSEL GEAR RIGGING DOORS YEAR MONTH DAY
#> 1 TA ITA 10 PEC GOC73 GC73 WHS8 2007 8 11
#> 2 TA ITA 10 PEC GOC73 GC73 WHS8 2007 8 11
#> 3 TA ITA 10 PEC GOC73 GC73 WHS8 2007 8 11
#> 4 TA ITA 10 PEC GOC73 GC73 WHS8 2007 8 11
#> 5 TA ITA 10 PEC GOC73 GC73 WHS8 2007 8 11
#> 6 TA ITA 10 PEC GOC73 GC73 WHS8 2007 8 11
#> HAUL_NUMBER CODEND_CLOSING PART_OF_THE_CODEND SHOOTING_TIME
#> 1 1 S S 1114
#> 2 2 S S 948
#> 3 3 S S 1500
#> 4 4 S S 1355
#> 5 5 S S 502
#> 6 6 S S 615
#> SHOOTING_QUADRANT SHOOTING_LATITUDE SHOOTING_LONGITUDE SHOOTING_DEPTH
#> 1 1 40.96233 13.66683 376
#> 2 1 41.03167 13.69167 109
#> 3 1 40.90900 13.82950 113
#> 4 1 40.95750 13.78783 95
#> 5 1 40.81617 13.96200 77
#> 6 1 40.91733 13.93683 25
#> HAULING_TIME HAULING_QUADRANT HAULING_LATITUDE HAULING_LONGITUDE
#> 1 1214 1 40.92067 13.70017
#> 2 1018 1 41.01117 13.70483
#> 3 1530 1 40.88800 13.85900
#> 4 1425 1 40.94050 13.80650
#> 5 532 1 40.83967 13.95783
#> 6 645 1 40.90317 13.91733
#> HAULING_DEPTH HAUL_DURATION VALIDITY COURSE RECORDED_SPECIES DISTANCE
#> 1 331 60 V R 3 5500
#> 2 112 30 V R 3 2593
#> 3 119 30 V R 3 2926
#> 4 97 30 V R 3 2500
#> 5 75 30 V R 3 2759
#> 6 23 30 V R 3 2630
#> VERTICAL_OPENING WING_OPENING GEOMETRICAL_PRECISION BRIDLES_LENGTH
#> 1 19 191 E 150
#> 2 19 182 E 100
#> 3 19 182 E 100
#> 4 19 182 E 100
#> 5 19 182 E 100
#> 6 19 163 E 100
#> WARP_LENGTH WARP_DIAMETER HYDROLOGICAL_STATION OBSERVATIONS
#> 1 1300 14 0 0
#> 2 550 14 0 0
#> 3 550 14 0 0
#> 4 550 14 0 0
#> 5 450 14 0 0
#> 6 300 14 0 0
#> BOTTOM_TEMPERATURE_BEGINNING BOTTOM_TEMPERATURE_END MEASURING_SYSTEM
#> 1 14.0 14.0 VA
#> 2 14.3 14.2 VA
#> 3 14.3 14.0 VA
#> 4 14.6 14.3 VA
#> 5 14.9 14.9 VA
#> 6 18.1 18.6 VA
#> NUMBER_OF_THE_STRATUM BOTTOM_SALINITY_BEGINNING BOTTOM_SALINITY_END
#> 1 13404 NA NA
#> 2 13403 NA NA
#> 3 13403 NA NA
#> 4 13402 NA NA
#> 5 13402 NA NA
#> 6 13401 NA NA
#> MEASURING_SYSTEM_SALINITY
#> 1 NA
#> 2 NA
#> 3 NA
#> 4 NA
#> 5 NA
#> 6 NA
# Coordinates conversion from decimal degrees to MEDITS format
med <- dd.to.MEDITS(dd)
head(med)
#> TYPE_OF_FILE COUNTRY AREA VESSEL GEAR RIGGING DOORS YEAR MONTH DAY
#> 1 TA ITA 10 PEC GOC73 GC73 WHS8 2007 8 11
#> 2 TA ITA 10 PEC GOC73 GC73 WHS8 2007 8 11
#> 3 TA ITA 10 PEC GOC73 GC73 WHS8 2007 8 11
#> 4 TA ITA 10 PEC GOC73 GC73 WHS8 2007 8 11
#> 5 TA ITA 10 PEC GOC73 GC73 WHS8 2007 8 11
#> 6 TA ITA 10 PEC GOC73 GC73 WHS8 2007 8 11
#> HAUL_NUMBER CODEND_CLOSING PART_OF_THE_CODEND SHOOTING_TIME
#> 1 1 S S 1114
#> 2 2 S S 948
#> 3 3 S S 1500
#> 4 4 S S 1355
#> 5 5 S S 502
#> 6 6 S S 615
#> SHOOTING_QUADRANT SHOOTING_LATITUDE SHOOTING_LONGITUDE SHOOTING_DEPTH
#> 1 1 4057.74 1340.01 376
#> 2 1 4101.90 1341.50 109
#> 3 1 4054.54 1349.77 113
#> 4 1 4057.45 1347.27 95
#> 5 1 4048.97 1357.72 77
#> 6 1 4055.04 1356.21 25
#> HAULING_TIME HAULING_QUADRANT HAULING_LATITUDE HAULING_LONGITUDE
#> 1 1214 1 4055.24 1342.01
#> 2 1018 1 4100.67 1342.29
#> 3 1530 1 4053.28 1351.54
#> 4 1425 1 4056.43 1348.39
#> 5 532 1 4050.38 1357.47
#> 6 645 1 4054.19 1355.04
#> HAULING_DEPTH HAUL_DURATION VALIDITY COURSE RECORDED_SPECIES DISTANCE
#> 1 331 60 V R 3 5500
#> 2 112 30 V R 3 2593
#> 3 119 30 V R 3 2926
#> 4 97 30 V R 3 2500
#> 5 75 30 V R 3 2759
#> 6 23 30 V R 3 2630
#> VERTICAL_OPENING WING_OPENING GEOMETRICAL_PRECISION BRIDLES_LENGTH
#> 1 19 191 E 150
#> 2 19 182 E 100
#> 3 19 182 E 100
#> 4 19 182 E 100
#> 5 19 182 E 100
#> 6 19 163 E 100
#> WARP_LENGTH WARP_DIAMETER HYDROLOGICAL_STATION OBSERVATIONS
#> 1 1300 14 0 0
#> 2 550 14 0 0
#> 3 550 14 0 0
#> 4 550 14 0 0
#> 5 450 14 0 0
#> 6 300 14 0 0
#> BOTTOM_TEMPERATURE_BEGINNING BOTTOM_TEMPERATURE_END MEASURING_SYSTEM
#> 1 14.0 14.0 VA
#> 2 14.3 14.2 VA
#> 3 14.3 14.0 VA
#> 4 14.6 14.3 VA
#> 5 14.9 14.9 VA
#> 6 18.1 18.6 VA
#> NUMBER_OF_THE_STRATUM BOTTOM_SALINITY_BEGINNING BOTTOM_SALINITY_END
#> 1 13404 NA NA
#> 2 13403 NA NA
#> 3 13403 NA NA
#> 4 13402 NA NA
#> 5 13402 NA NA
#> 6 13401 NA NA
#> MEASURING_SYSTEM_SALINITY
#> 1 NA
#> 2 NA
#> 3 NA
#> 4 NA
#> 5 NA
#> 6 NATwo functions were also introduced to estimate the hauls distance using respectivelly MEDITS coordinates and decimal degrees coordinates:
library(MEDITS)
# distance estimation using MEDITS coordinates
med.dist <- MEDITS.distance(TA, unit="km", verbose=TRUE)
#> kilometers
head(med.dist)
#> [1] 5.409739 2.531317 3.403627 2.454159 2.634717 2.271499
# distance estimation using decimal degrees coordinates
dd <- MEDITS.to.dd(TA)
dd.dist <- dd.distance(dd, unit="km", verbose=TRUE)
#> kilometers
head(dd.dist)
#> [1] 5.409739 2.531317 3.403627 2.454159 2.634717 2.271499The function land.points allows to check whether some of the TA table’s coordinates fall on the land:
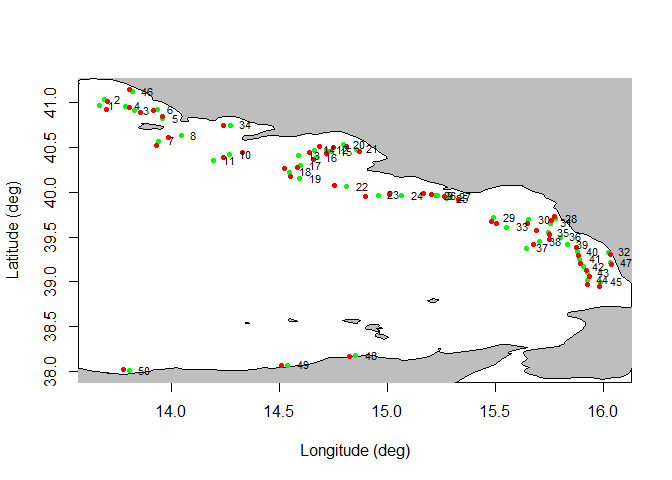
A plot of haul’s positions could also be generated, with the possibility to define the years range to be considered, the GSA area and, whether both initial and end coordinates should be plotted or only the mean haul coordinates:

To link the geographic information of the hauls respectively to catch and biological data were introduced two different functions: m.TATB and m.TATC:
# merge of TA and TB tables
mTATB <- m.TATB(TA,TB,"ARISFOL")
# merge of TA and TB tables
mTATC <- m.TATC(TA,TC,"ARISFOL")The estimation of the indices’ time series is performed by the index.ts function. It is possible to estimate the following indices: abundance, inverse of abundance CV, biomass and mean individual weight (MIW). The analysis could also be performed by sex.
merge_TATB <- m.TATB(TA,TB,"ARISFOL")
ind <- index.ts(merge_TATB, index="abundance", depth_range = c(500,800), sex="f",
str.scheme=strata_scheme, surf=stratification_scheme)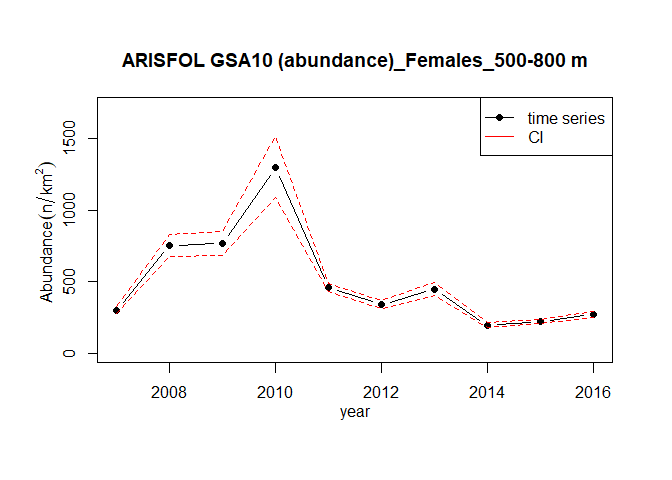
The function sexratio.ts estimates the time series of the sex ratio:
ind <- m.TATB(TA,TB,"ARISFOL")
sexratio.ts(merge = ind, GSA = NA, sspp = NA, depth_range=c(500,800),
strata_scheme=strata_scheme, stratification=stratification_scheme, plot=TRUE )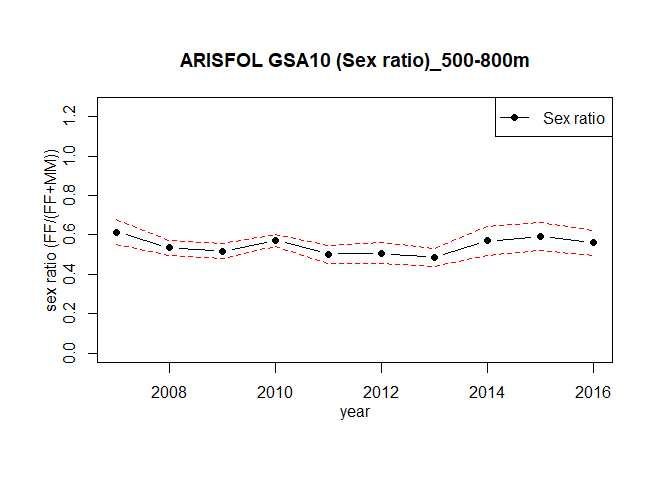
#> year Indices_F Indices_FM sex.ratio variance sd
#> 1 2007 299.2558 486.8133 0.6147239 0.0009996861 0.03161781
#> 2 2008 752.4499 1408.3255 0.5342869 0.0003541958 0.01882009
#> 3 2009 767.4742 1481.7511 0.5179508 0.0003372210 0.01836358
#> 4 2010 1299.4429 2274.6234 0.5712783 0.0002175715 0.01475031
#> 5 2011 457.9915 911.2554 0.5025940 0.0005486862 0.02342405
#> 6 2012 338.1038 667.3721 0.5066196 0.0007491415 0.02737045
#> 7 2013 446.7506 921.2462 0.4849416 0.0005424969 0.02329156
#> 8 2014 193.2033 339.2838 0.5694444 0.0014594096 0.03820222
#> 9 2015 222.5422 375.6135 0.5924765 0.0013081896 0.03616890
#> 10 2016 270.0096 481.6231 0.5606242 0.0010304969 0.03210135
#> positive_hauls_perc
#> 1 100
#> 2 100
#> 3 100
#> 4 100
#> 5 100
#> 6 100
#> 7 100
#> 8 100
#> 9 100
#> 10 100The function index.rs allows to estimate the time series of abundance index for both recruits and spawners:
index.rs (TA,TB,TC,GSA=10,sspp="ARISFOL",stage ="recruits",cutoff=29,
depth_range=c(500,800),str.scheme=strata_scheme,
surf=stratification_scheme,plot=TRUE)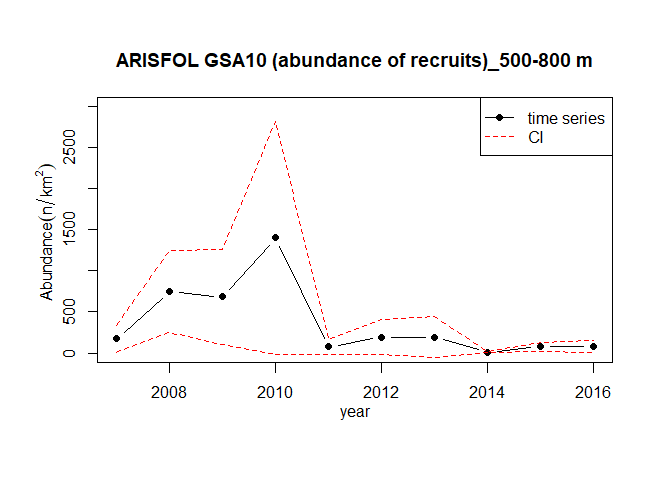
#> year abundance sd
#> 1 2007 173.819218 85.441493
#> 2 2008 746.525103 253.963668
#> 3 2009 682.000011 295.301758
#> 4 2010 1399.952318 724.374171
#> 5 2011 73.869603 44.097009
#> 6 2012 193.791201 106.736291
#> 7 2013 194.214778 125.944553
#> 8 2014 7.068412 3.177105
#> 9 2015 75.946935 28.093725
#> 10 2016 77.475985 38.404432Placing the above described indices in the spatial dimension is very useful for several objectives, as the knowledge of the distribution and abundance of the species at local and regional spatial scale, the identification of areas with certain peculiarities, the localization of sensitive life stage of the population, etc… GFCM grid is considered as the better available trade-off for the spatial scale to be used in the different steps of the analysis, especially considering the subsequent possible overlap with maps of the fishing effort spatial distribution. This despite the fact that not any unit in the grid can actually encompass the spatial distribution of all the life stages of a given species, especially when this distribution is depth related. To perform the spatial analysis of the indicators it is needed to assign the haul information to the relative cells of the GFCM statistical grid contained in cgpmgrid variable as SpatialPolygonsDataFrame. The functions TATB.grid and TATC.grid were generated with this purpose:
# overlap of TATB with the grid
gTATB <- TATB.grid(TA,TB,"ARISFOL")
# overlap of TATC with the grid
gTATC <- TATC.grid(TA,TC,"ARISFOL")The estimation of the indices over the statistical grid is performed by the function sp.index:
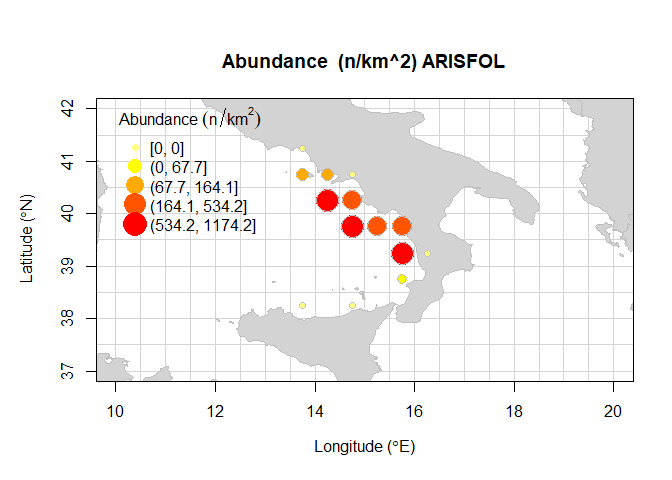
#> cgpmgridlevel GSA meanNkm2 sdNkm2 cvNkm2 inverse_cvNkm2 nhauls
#> 1 5091 10 0.00000 0.0000 NaN NaN 20
#> 2 5227 10 99.99893 329.7339 3.2973739 0.3032716 60
#> 3 5228 10 81.62708 230.6419 2.8255557 0.3539127 20
#> 4 5229 10 0.00000 0.0000 NaN NaN 11
#> 5 5364 10 1174.22674 1190.8150 1.0141270 0.9860698 20
#> 6 5365 10 180.12146 421.2692 2.3388063 0.4275685 99
#> 7 5501 10 1140.74609 928.8783 0.8142726 1.2280899 10
#> 8 5502 10 433.82575 1009.3968 2.3267333 0.4297871 57
#> 9 5503 10 479.51507 1678.8692 3.5011814 0.2856179 63
#> 10 5639 10 616.35084 626.4636 1.0164075 0.9838574 83
#> 11 5640 10 0.00000 0.0000 NaN NaN 20
#> 12 5775 10 64.19004 121.4411 1.8919000 0.5285692 7
#> 13 5907 10 0.00000 0.0000 NaN NaN 10
#> 14 5909 10 0.00000 0.0000 NaN NaN 20
#> positive_hauls lon lat
#> 1 0 13.75 41.25
#> 2 11 13.75 40.75
#> 3 4 14.25 40.75
#> 4 0 14.75 40.75
#> 5 20 14.25 40.25
#> 6 27 14.75 40.25
#> 7 10 14.75 39.75
#> 8 17 15.25 39.75
#> 9 13 15.75 39.75
#> 10 81 15.75 39.25
#> 11 0 16.25 39.25
#> 12 2 15.75 38.75
#> 13 0 13.75 38.25
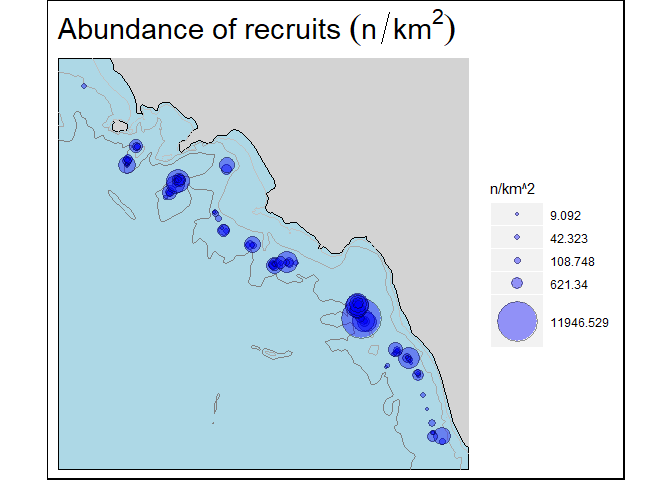
#> 14 0 14.75 38.25Furthermore, the function bubble.rs, using TA, TB, and TC tables estimates the abundance indices per hauls for recruits and spawners specimens. Recruits and spawners specimens are selected using the cutoff parameter defined by the user. Bathymetrical lines refers respectively to 50m, 200m, and 800m of depth.
The different percentiles of a length frequency distribution (LFD) are expected to respond differently to fishing, recruitment pulses, and loss of spawning stock. It is assumed to be negatively (decrease) affected by an excessive fishing pressure.
Length frequency distribution (LFD) is computed by the LFD function, while the Lq is estimated by quant function:
merge_TATB <- m.TATB(TA,TB,"ARISFOL")
merge_TATC <- m.TATC(TA,TC,"ARISFOL")
indices <- index.ts(merge_TATB,GSA = 10 ,"ARISFOL",index = "abundance",
depth_range=c(500,800), str.scheme=strata_scheme,
surf=stratification_scheme, sampling = "RSS",plot=FALSE)
freq <- LFD(merge_TATC,indices,sex="m",LC=1,depth_range=c(500,800), type = "indices")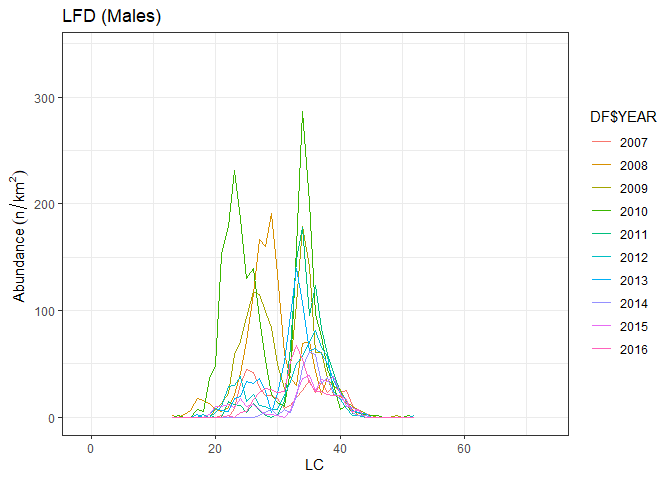
quant(freq,0.95)
#> 2007 2008 2009 2010 2011 2012 2013 2014 2015 2016
#> percentile 40.90 37.80 38.70 36.90 39.00 38.80 39.30 40.30 40.60 40.10
#> Variance 0.04 0.14 0.05 0.01 0.02 0.01 0.03 0.05 0.04 0.06In presence of a short trawl survey time series the significance of the trend can be estimated using nonparametric statistical tests as Spearman rho (Cotter, 2009). Spearman’s rho is the product-moment correlation between the ranks of paired data. The spearman.test function perform the Spearman test of the trend on the indices time series: